封面画师:Nengoro(ネんごろぅ) 封面ID:66613178
本文参考视频:小马哥教育(SEEMYGO) 2019年 恋上数据结构与算法(第二季)
源码仓库:mofan212/data-structure-and-algorithm (github.com)
1. 分治
1.1 基本含义
分治,英文 Divide And Conquer,意为分开并战胜,即分而治之、分治。
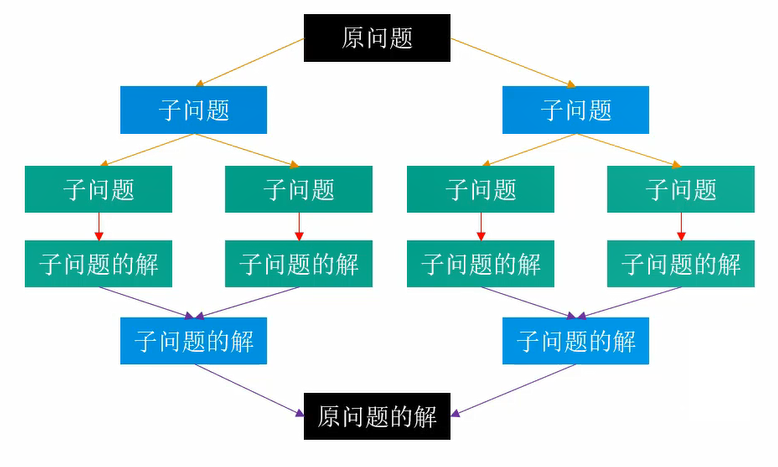
分治的一般步骤是:
将原问题分解成若干个规模较小的子问题(子问题和原问题的结构一样,只是规模不一样);
子问题又不断分解成规模更小的子问题,直到不能再分解(直到可以轻易计算出子问题的解);
利用子问题的解推导出原问题的解。
因此分治策略非常适合用递归。
注意: 子问题之间是相互独立的。
分治的应用:
快速排序
归并排序
Karatsuba 算法(大数乘法)
1.2 Master Theorem
Master Theorem,即主定理。
分治通常遵守一种通用模式。解决规模为 n 的问题,分解成 a 个规模为 n b \frac{n}{b} b n O ( n d ) O(n^d) O ( n d )
算法运行时间为:T ( n ) = a T ( n b ) + O ( n d ) , a > 0 , b > 1 , d ≥ 0 T(n) = aT(\frac{n}{b}) + O(n^d), \quad a \gt 0, \quad b \gt 1, \quad d \ge 0 T ( n ) = a T ( b n ) + O ( n d ) , a > 0 , b > 1 , d ≥ 0
针对以上公式有:
d > l o g b a , T ( n ) = O ( n d ) d \gt log_ba, \quad T(n) = O(n^d) d > l o g b a , T ( n ) = O ( n d ) d = l o g b a , T ( n ) = O ( n d l o g n ) d = log_ba, \quad T(n) = O(n^dlog_n) d = l o g b a , T ( n ) = O ( n d l o g n ) d < l o g b a , T ( n ) = O ( n l o g b a ) d \lt log_ba, \quad T(n) = O(n^{log_ba}) d < l o g b a , T ( n ) = O ( n l o g b a )
比如归并排序的运行时间是:T ( n ) = 2 T ( n 2 ) + O ( n ) T(n) = 2T(\frac{n}{2}) + O(n) T ( n ) = 2 T ( 2 n ) + O ( n ) a = 2 , b = 2 , d = 1 a = 2, b = 2, d = 1 a = 2 , b = 2 , d = 1 T ( n ) = O ( n l o g n ) T(n) = O(nlogn) T ( n ) = O ( n l o g n )
2. 分治的练习
2.1 最大连续子序列和
来源 LeetCode 第 53 题:最大子数组和
给定一个长度为 n 的整数序列,求它的最大连续子序列和。比如 –2、1、–3、4、–1、2、1、–5、4 的最大连续子序列和是 4 + ( – 1 ) + 2 + 1 = 6 4 + (–1) + 2 + 1 = 6 4 + ( –1 ) + 2 + 1 = 6
这道题也属于最大切片问题(最大区段,Greatest Slice)。
概念拓展:子串、子数组、子区间必须是连续的,子序列是可以不连续的。
暴力出奇迹
穷举出所有可能的连续子序列,并计算出它们的和,最后取它们中的最大值。
思路解释:提供两个指针 A、B,最开始时 A 和 B 都指向数组中的第一个元素,之后 A 保持不动,B 每次以步长 1 向数组末尾移动,每次移动时计算由 A 到 B 之间组成的子序列之和,保存最大的和,直到 B 指向数组末位元素。然后 A 向后移动一位,B 也指向相同的位置,重复先前的操作,每次求得的子序列和都和保存的最大的和进行比较,不断更新最大的值,直到 A 和 B 都指向数组的末位。
不难写出以下代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public class SubArray { public static void main (String[] args) { int [] nums = {-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 }; System.out.println(maxSubArray(nums)); } static int maxSubArray (int [] nums) { if (nums == null || nums.length == 0 ) { return 0 ; } int max = Integer.MIN_VALUE; for (int begin = 0 ; begin < nums.length; begin++) { for (int end = begin; end < nums.length; end++) { int sum = 0 ; for (int i = begin; i < end; i++) { sum += nums[i]; } max = Math.max(max, sum); } } return max; } }
不难看出这段代码的时间复杂度是 O ( n 3 ) O(n^3) O ( n 3 )
尽管是暴力求解,但也还有可以优化的地方。上方代码在每次求取 begin 到 end 之间的子序列和时都进行了重复运算,完全不需要每次都从头遍历求和,因为本次的子序列之和就是上次子序列之和加上当前 end 指向的元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 static int maxSubArray (int [] nums) { if (nums == null || nums.length == 0 ) { return 0 ; } int max = Integer.MIN_VALUE; for (int begin = 0 ; begin < nums.length; begin++) { int sum = 0 ; for (int end = begin; end < nums.length; end++) { sum += nums[end]; max = Math.max(max, sum); } } return max; }
优化后的时间复杂度是 O ( n 2 ) O(n^2) O ( n 2 )
分治法
将序列均匀地分割成 2 个子序列:
[ b e g i n , e n d ) = [ b e g i n , m i d ) + [ m i d , e n d ) , m i d = ( b e g i n + e n d ) > > 1 [begin, end) = [begin, mid) + [mid, end), \quad mid = (begin + end) \gt\gt 1 [ b e g in , e n d ) = [ b e g in , mi d ) + [ mi d , e n d ) , mi d = ( b e g in + e n d ) >> 1
假设问题的解是 S [ i , j ) S[i, j) S [ i , j )
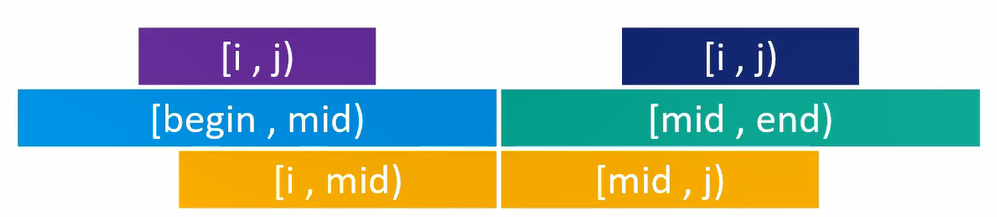
[ i , j ) [i, j) [ i , j ) [ b e g i n , m i d ) [begin, mid) [ b e g in , mi d ) [ i , j ) [i, j) [ i , j ) [ m i d , e n d ) [mid, end) [ mi d , e n d ) [ i , j ) [i, j) [ i , j ) [ b e g i n , m i d ) [begin, mid) [ b e g in , mi d ) [ m i d , e n d ) [mid, end) [ mi d , e n d )
[ i , j ) = [ i , m i d ) + [ m i d , j ) [i, j) = [i, mid) + [mid, j) [ i , j ) = [ i , mi d ) + [ mi d , j ) [ i , m i d ) = m a x { S [ k , m i d ) } , b e g i n ≤ k < m i d [i, mid) = max\{S[k, mid)\},\quad begin \le k \lt mid [ i , mi d ) = ma x { S [ k , mi d )} , b e g in ≤ k < mi d
也就是说,以 mid 为分割线,求出左边最大的子序列和、求出右边最大的子序列和、求出横跨左右两边的最大子序列和,在这三个子序列和中选取最大的就是此题的解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public static void main (String[] args) { int [] nums = {-2 , 1 , -3 , 4 , -1 , 2 , 1 , -5 , 4 }; System.out.println(maxSubArray(nums, 0 , nums.length)); } static int maxSubArray (int [] nums, int begin, int end) { if (end - begin < 2 ) { return nums[begin]; } int mid = (begin + end) >>> 1 ; int leftMax = nums[mid - 1 ]; int leftSum = 0 ; for (int i = mid - 1 ; i >= begin; i--) { leftSum += nums[i]; leftMax = Math.max(leftMax, leftSum); } int rightMax = nums[mid]; int rightSum = 0 ; for (int i = mid; i < end; i++) { rightSum += nums[i]; rightMax = Math.max(rightMax, rightSum); } return Math.max( leftMax + rightMax, Math.max( maxSubArray(nums, begin, mid), maxSubArray(nums, mid, end) ) ); }
上述代码的时间复杂度即为解的三种可能的时间复杂度之和:
求出左边最大的子序列和的时间复杂度是:T ( n 2 ) T(\frac{n}{2}) T ( 2 n )
求出右边最大的子序列和的时间复杂度是:T ( n 2 ) T(\frac{n}{2}) T ( 2 n )
求出横跨左右两边的最大子序列和的时间复杂度是:T ( n ) T(n) T ( n )
这些很好理解,求出左右两边的子序列的时间复杂度是折半的,因此都为 T ( n 2 ) T(\frac{n}{2}) T ( 2 n ) O ( n ) O(n) O ( n )
代码整体的时间复杂度是:T ( n ) = 2 T ( n 2 ) + O ( n ) T(n)=2T(\frac{n}{2})+O(n) T ( n ) = 2 T ( 2 n ) + O ( n ) T ( n ) = O ( n l o g n ) T(n) = O(nlogn) T ( n ) = O ( n l o g n )
2.2 大数乘法
本节只讲理论,不讲实现!
2 个超大的数(比如 2 个 100 位的数),如何进行乘法而不会数据溢出呢?
按照学习的乘法运算,在进行 n 位数之间的相乘时,大约需要进行 n 2 n^2 n 2
比如计算 36 × 54 36 \times 54 36 × 54
一共进行了 4 次个位数的相乘,并且时间复杂度是 O ( n 2 ) O(n^2) O ( n 2 )
时间复杂度是怎么计算的呢?
根据图示可知,将 n 位数与 n 位数的相乘可以看成 n 2 + n 2 \frac{n}{2} + \frac{n}{2} 2 n + 2 n n 2 + n 2 \frac{n}{2} + \frac{n}{2} 2 n + 2 n 4 T ( n 2 ) 4T(\frac{n}{2}) 4 T ( 2 n ) O ( n ) O(n) O ( n )
最终得到的时间复杂度是 T ( n ) = 4 T ( n 2 ) + O ( n ) T(n)=4T(\frac{n}{2})+O(n) T ( n ) = 4 T ( 2 n ) + O ( n ) O ( n 2 ) O(n^2) O ( n 2 )
Karatsuba 算法
1960 年 Anatolii Alexeevitch Karatsuba 提出了 Karatsuba 算法,提高了大数乘法的效率。
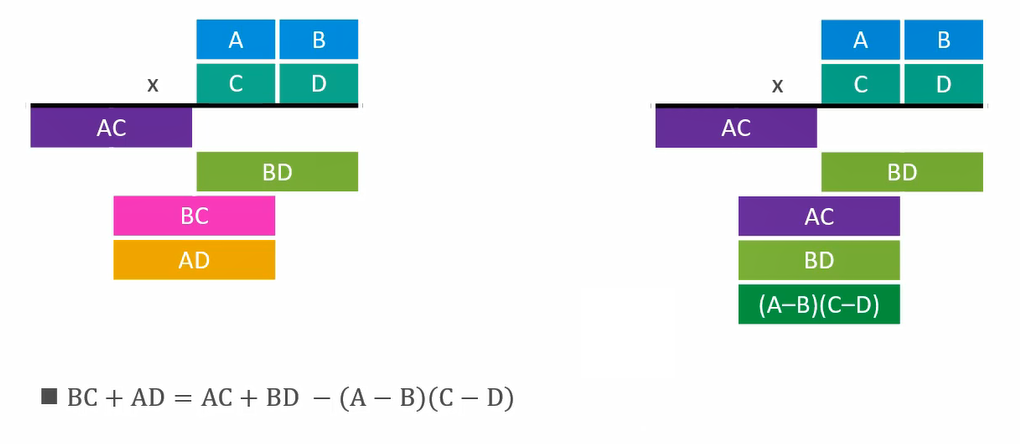
他发现 B C + A D = A C + B D − ( A − B ) ( C − D ) BC + AD = AC + BD - (A - B)(C - D) BC + A D = A C + B D − ( A − B ) ( C − D )
那修改后的时间复杂度是多少?
A C AC A C B D BD B D T ( n 2 ) T(\frac{n}{2}) T ( 2 n ) ( A − B ) ( C − D ) (A - B)(C - D) ( A − B ) ( C − D )
最坏情况下,A − B A - B A − B A A A C − D C - D C − D C C C ( A − B ) ( C − D ) (A - B)(C - D) ( A − B ) ( C − D ) A C AC A C B D BD B D T ( n 2 ) T(\frac{n}{2}) T ( 2 n )
因此可得时间复杂度为 T ( n ) = 3 T ( n 2 ) + O ( n ) T(n)=3T(\frac{n}{2})+O(n) T ( n ) = 3 T ( 2 n ) + O ( n ) T ( n ) = O ( n l o g 2 3 ) T(n)=O(n^{log_23}) T ( n ) = O ( n l o g 2 3 ) O ( n 1.585 ) O(n^{1.585}) O ( n 1.585 ) O ( n 2 ) O(n^2) O ( n 2 )