封面画师：Nengoro(ネんごろぅ)     封面ID：74731465

本文参考视频：小马哥教育(SEEMYGO) 2019年 恋上数据结构与算法（第二季）

源码仓库：mofan212/data-structure-and-algorithm (github.com)

辅助学习网址：数据结构和算法动态可视化     Data Structure Visualizations

执行流程：本文统一以升序为例子。

1. 快速排序

1.1 前言

在前一篇文章中，谈到了归并排序，知道了归并排序的时间复杂度为O(nlogn)。在初学排序算法时，谈到了堆排序，堆排序的时间复杂度也是O(nlogn)。那么还有其他的排序算法的时间复杂度也是O(nlogn)吗？当然是有的，快速排序就是。

听到这名字，快速排序，感觉就很厉害的样子。

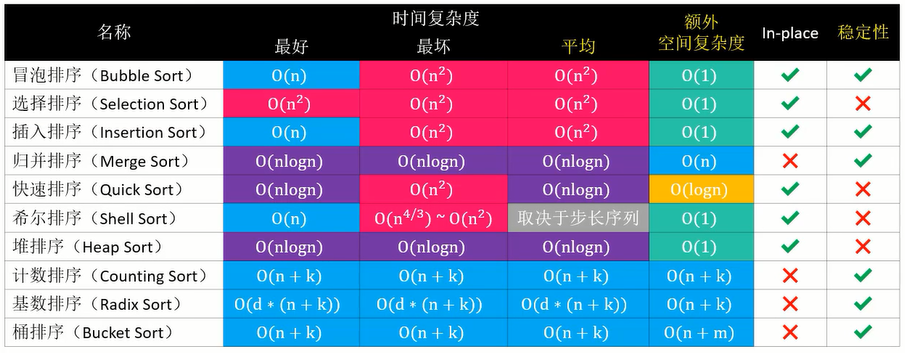
十大排序算法

从上图中，我们可以看到，快速排序的最好、平均时间复杂度为 O(nlogn) ，但是最坏时间复杂度是 O(n2) ，最坏时间复杂度赶不上归并排序和堆排序，那要是经常遇到最坏情况，效率岂不是也很低？怎么对得起快速二字呢？

虽然快速排序的最坏时间复杂度是 O(n2)，但是我们有办法减低最坏情况出现的概率，总体来说快速排序的效率还是很高的。

相比于平均时间复杂度也为O(nlogn)的归并排序和堆排序，快速排序会 “ 更快 ” 一点！

1.2 执行流程

快速排序（Quick Sort），1960年由查尔斯·安东尼·理查德·霍尔（Charles Antony Richard Hoare，缩写为 C.A.R.Hoare）提出，昵称为东尼·霍尔（一译托尼·霍尔，英语：Tony Hoare）。

TonyHoare

这又是一位大佬，曾在1980年获颁图灵奖、在2011年获颁约翰·冯诺依曼奖。

执行流程

1、从序列中选择一个轴点元素（pivot）

  • 假设每次选择 0 位置的元素为轴点元素

2、利用 pivot 将序列分割成 2 个子序列

  • 将小于 pivot 的元素放在 pivot 前面（左侧）
  • 将大于 pivot 的元素放在 pivot 后面（右侧）
  • 等于 pivot 的元素放在哪边都可以

3、对子序列进行 ① ②操作

  • 直到不能再分割（子序列中只剩下 1 个元素）

快速排序执行流程图：

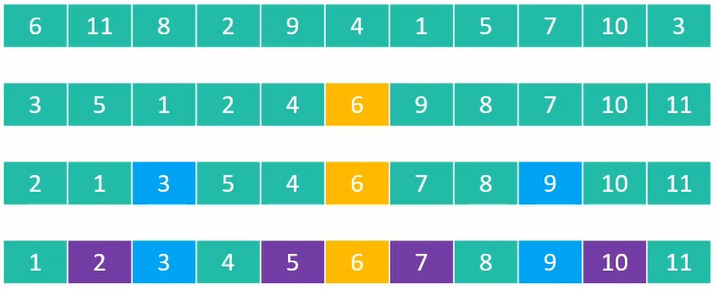
快速排序执行流程图

快速排序执行动图：

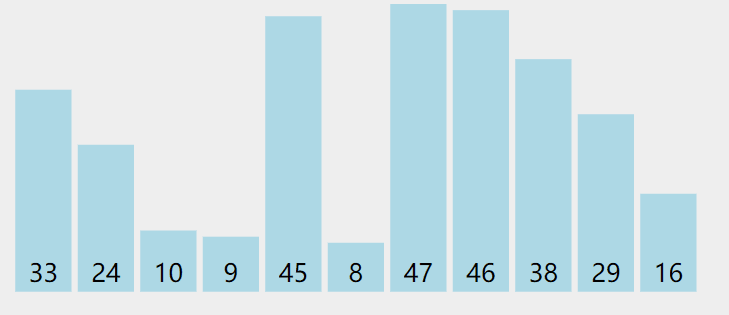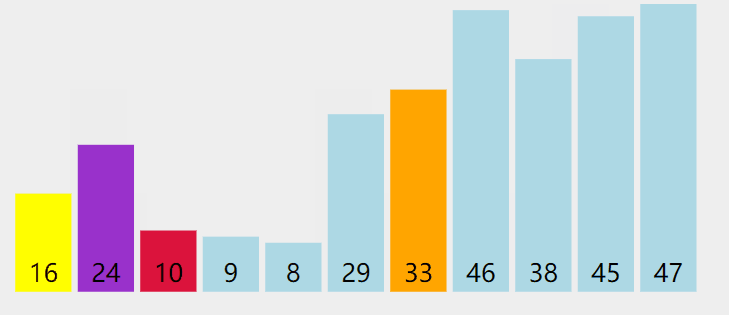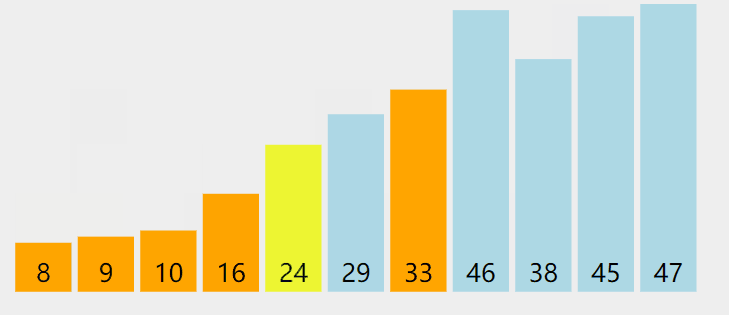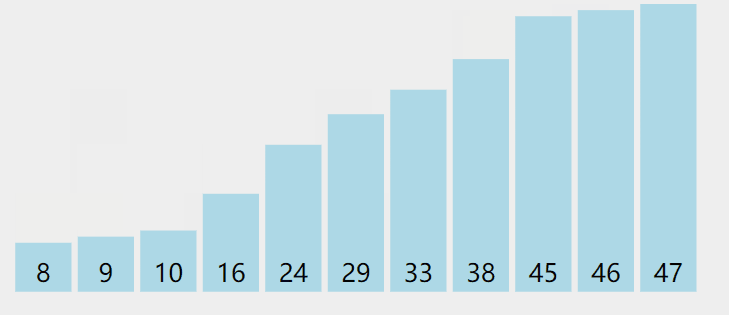
QuickSort

快速排序的本质：逐渐将每一个元素都转换成轴点元素。

既然如此我们就要先搞清楚 0 位置的元素是怎么变成轴点的。

1.3 轴点构造

先选择序列中 0 位置的元素作为轴点元素，然后设置两个指针begin和end，其中begin指向序列首元素，end指向序列尾元素。

我们以前在设计时常将 end 设置为序列的长度，在这里我们也可以将其设置为序列的长度，但是为了使用 end 指针，在使用前需要将 end 向后移一位，即：将 end 指向序列尾元素。

选择好轴点元素后，我们还需要将其备份一份。

然后我们先从序列右边开始遍历（先从end向begin遍历），比较遍历元素与轴点元素的大小关系：

  • 当 end 指向的元素大于轴点元素时， end--
  • 当 end 指向的元素小于等于轴点元素时，end 不变，用 end 指向的元素覆盖 begin 指向的元素，然后begin++

每当一个元素位置被确定时，我们就需要从相反方向进行遍历（从begin到end遍历），比较遍历元素与轴点元素的大小关系：

  • 当 begin 指向的元素大于轴点元素时， begin 不变，用 begin 指向的元素覆盖 end 指向的元素，然后end--
  • 当 begin 指向的元素小于等于轴点元素时， begin++

重复进行以上操作，直到 begin == end 的时候，在这个时候我们用备份的元素覆盖 begin 和 end 指向的元素，这样一个轴点就构造出来了。

快速排序轴点构造流程

上面的图示仅仅介绍了构造第一个轴点，如果我们需要对整个序列进行排序，相当于需要将每个元素都转换成轴点元素。

当我们确定了第一个轴点后，我们需要在轴点左右两边的序列中确认第二个、第三个轴点，然后又在确认的轴点左右两边确认新的轴点，确认轴点的过程也相当于一次快速排序。

这其实和归并排序很类似，属于一种递归。

1.4 编码实现

我们发现，快速排序和归并排序类似，也可以采用递归的方式。先理一下思路：

1、备份 begin 位置的元素，然后确认第一个轴点

2、在上一步确认的轴点两边重复上一步操作，直到每个元素都转换成轴点元素

上述步骤可以看成一个递归的过程。那么重点就是如何确认轴点了，而我们在上一节中已经分析的轴点的确认方法。

快速排序编码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/**
 * @author 默烦
 * @date 2020/8/16
 */
public class QuickSort<E extends Comparable<E>> extends Sort<E> {
    @Override
    protected void sort() {
        sort(0, array.length);
    }

    /**
     * 对 [begin, end) 范围的元素进行快速排序
     * @param begin 序列开始位置索引
     * @param end 序列长度
     */
    private void sort(int begin, int end){
        if (end - begin < 2) return;
        // 确定轴点位置
        int p = pivot(begin, end);
        // 对子序列进行快速排序
        sort(begin, p);
        sort(p + 1, end);
    }

    /**
     *  构造出 [begin, end) 范围的轴点元素
     * @param begin 序列开始位置索引
     * @param end 序列长度
     * @return 轴点元素的最终位置
     */
    private int pivot(int begin, int end){
        // 备份 begin 位置的元素
        E pivot = array[begin];
        // end 指向最后一个元素
        end--;
        while (begin < end){
            while (begin < end){
                if (cmp(pivot, array[end]) < 0){ // 右边元素 > 轴点元素
                    end--;
                } else { // 右边元素 <= 轴点元素
                    array[begin++] = array[end];
                    // 赋值后换方向遍历
                    break;
                }
            }

            while (begin < end){
                if (cmp(pivot, array[begin]) > 0){ // 左边元素 < 轴点元素
                    begin++;
                } else { // 左边元素 >= 轴点元素
                    array[end--] = array[begin];
                    // 赋值后换方向遍历
                    break;
                }
            }
        }

        // 将轴点元素放入
        array[begin] = pivot;
        // 返回轴点元素的位置
        return begin;
    }
}

代码编写完成后，我们可以进行测试，对时间复杂度为O(nlogn)的三个方法进行测试。

生成 5w 个随机数，范围是[1, 50000] ，方法耗时如下：

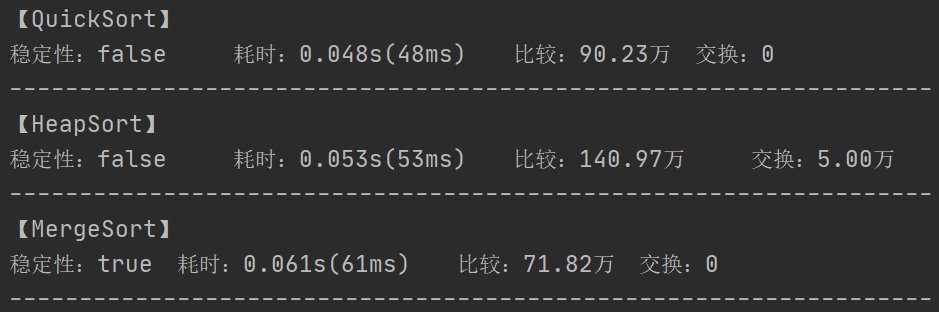
快速排序测试对比

根据测试结果，我们可以看到快速排序还是很优秀的，当然不同的硬件、不同的序列可能会导致这三种的耗时排序发生变化。

1.5 时间复杂度

最好的情况

对于快速排序，如果轴点左右元素数量比较均匀（各占一半）的情况下，也就是最好的情况。

因为快速排序用了递归，我们可以像分析归并排序的时间复杂度一样，使用递推公式来计算归并排序的时间复杂度。

快速排序最好情况递推公式

这个递推公式很眼熟，跟分析归并排序时的递推公式一样。

因此，在最好情况下，快速排序的时间复杂度为O(nlogn)。

最坏的情况

对于快速排序，如果轴点左右元素数量极度不均匀，也就是最坏的情况。

快速排序最坏情况图解：

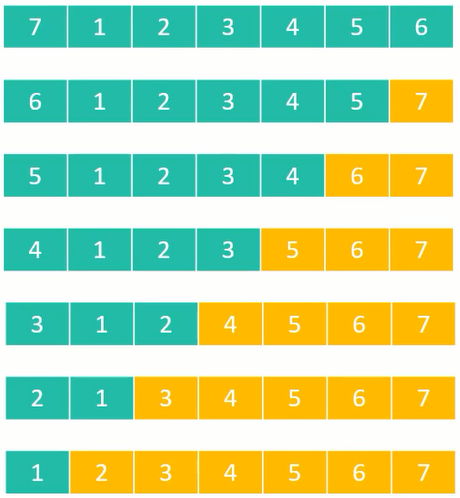
快速排序最坏情况图解

那么在这种情况下的时间复杂度是多少呢？我们依旧通过递推公式来计算。

快速排序最坏情况递推公式

有了递推公式，我们可以求得其时间复杂度为： O(n2)

常见的递推式与复杂度

降低最坏情况出现概率

既然最坏情况下时间复杂度这么高，那有什么解决的办法吗？

为了降低最坏情况的出现概率，一般采取的做法是：

  • 随机选择轴点元素

简单来说，我们可以用 begin 位置的元素与当前序列除 begin 位置外的其他元素进行交换即可。

代码修改也很简单，只需要对pivot()方法最开始的位置添加一句代码就可以实现随机选择轴点位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 *  构造出 [begin, end) 范围的轴点元素
 * @param begin 序列开始位置索引
 * @param end 序列长度
 * @return 轴点元素的最终位置
 */
private int pivot(int begin, int end){
    // 随机选择一个元素跟begin位置进行交换
    swap(begin, begin + (int) (Math.random() * (end - begin)));

    // 备份 begin 位置的元素
    E pivot = array[begin];
    // end 指向最后一个元素
    end--;
    while (begin < end){
        while (begin < end){
            if (cmp(pivot, array[end]) < 0){ // 右边元素 > 轴点元素
                end--;
            } else { // 右边元素 <= 轴点元素
                array[begin++] = array[end];
                // 赋值后换方向遍历
                break;
            }
        }

        while (begin < end){
            if (cmp(pivot, array[begin]) > 0){ // 左边元素 < 轴点元素
                begin++;
            } else { // 左边元素 >= 轴点元素
                array[end--] = array[begin];
                // 赋值后换方向遍历
                break;
            }
        }
    }

    // 将轴点元素放入
    array[begin] = pivot;
    // 返回轴点元素的位置
    return begin;
}

总结

最好、最坏的时间复杂度为： O(nlogn)

最坏时间复杂度为： O(n2)

由于递归调用的缘故，空间复杂度为： O(logn)

快速排序属于不稳定排序（我们从轴点构造流程图也可以看出来）。

1.6 轴点相等元素

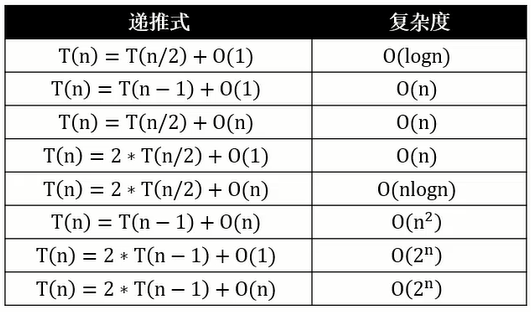
在前面编写的代码中，确认轴点（获取轴点位置）时，有一段下图所示的代码：

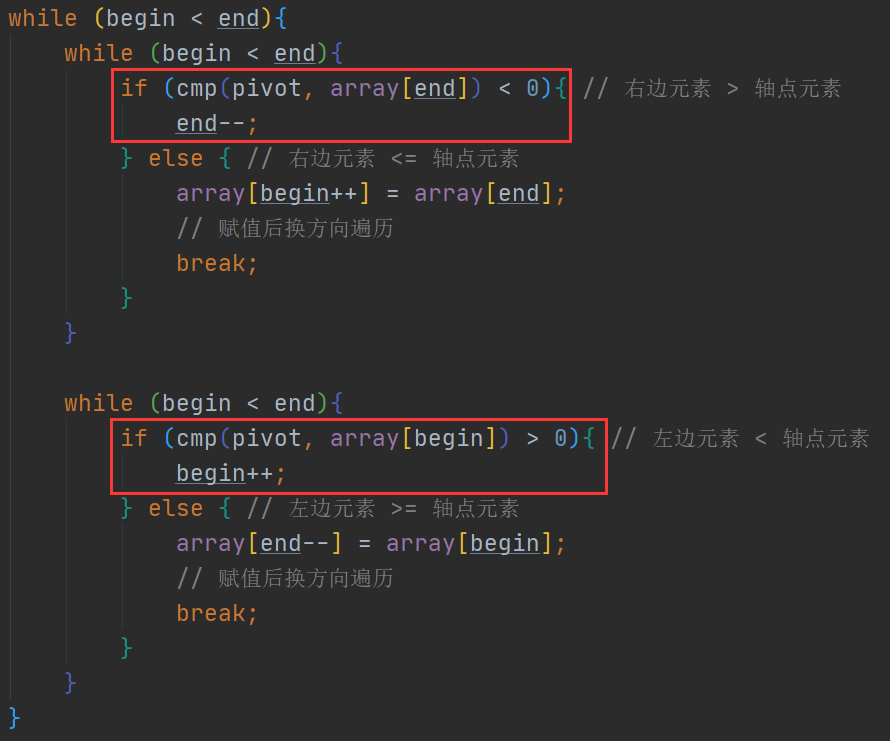
与轴点相等元素的处理代码

在上图中，两个矩形圈出的代码中不含相等判断，就是说当选中元素与轴点相等时，我们会将选中元素赋值到另一边的子序列中。

语言阐述可能有些问题，那么可以查看下面的示意图：

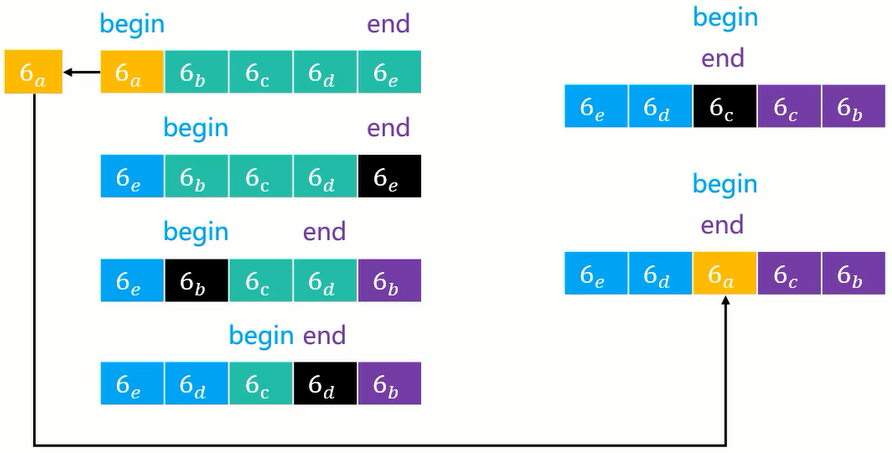
与轴点相等元素处理示意图

从上图中可以看到，如果所有序列中的所有元素都与轴点元素相等，利用当前的算法实现，轴点元素可以将序列分成 2 个均匀的子序列。

拓展思考

如果将 cmp() 位置的判断分别改成 >= 、<= 会起到什么效果呢？

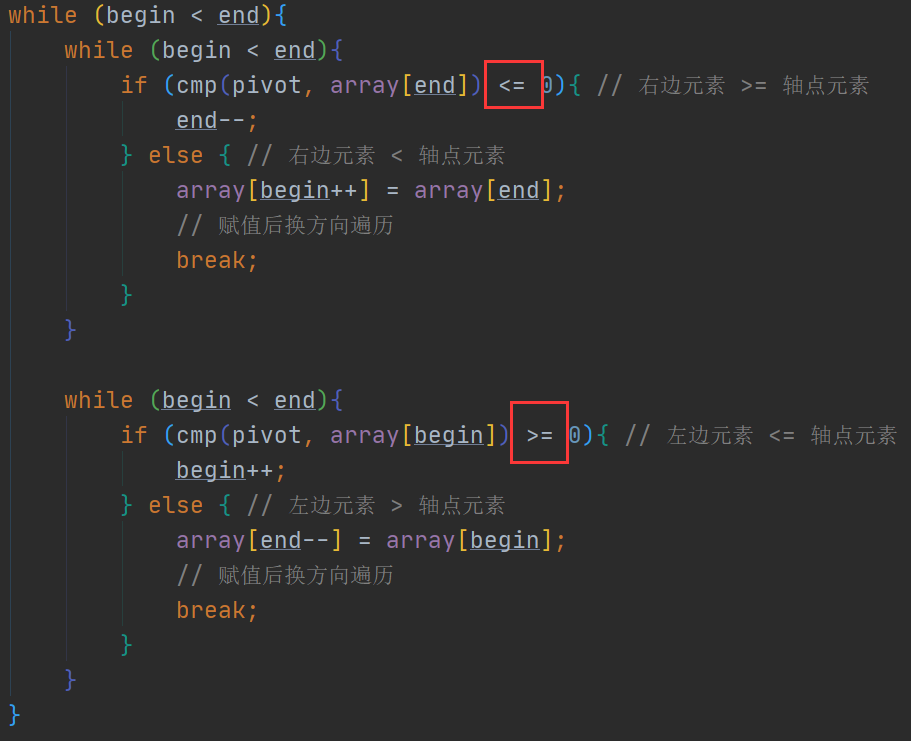
快速排序添加相等判断

在cmp()方法中添加相等判断后，如果选中元素与轴点相等时，我们直接改变索引，而不进行赋值转向。

比较方法添加相等判断示意图：

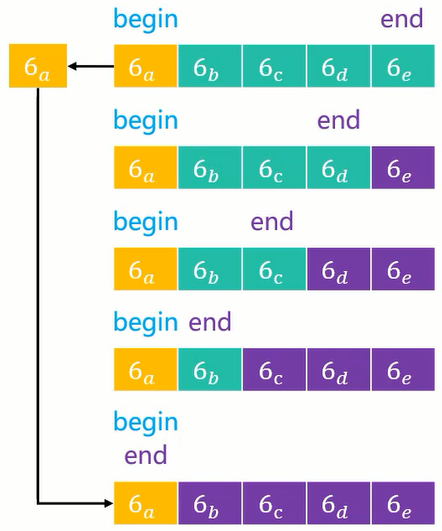
比较方法添加相等判断示意图

添加相等判断后，轴点元素分割出来的子序列极其不均匀，导致出现最坏时间复杂度 O(n2) 。

我们可以进行测试一下，使用快速排序对 1w 个相同的数进行排序：

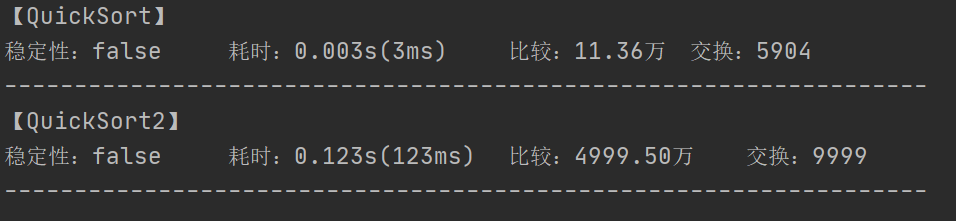
快速排序添加相等对比测试

第一种是未添加相等判断的，第二种是添加了相等判断的，我们可以看出，添加前后耗时相差甚远，后者耗时近乎是前者的 40 倍，损失了相当多的效率。

如果进一步扩大数据规模，比如对 5w 个相等的数进行快速排序，第二种情况很有可能出现StackOverflowError异常。

因此，我们在编写代码时，不要在比较元素时添加相等判断。

2. 希尔排序

2.1 概念介绍

希尔排序（Shell Sort），由唐纳德·刘易斯·希尔（Donald Lewis Shell）在1959年提出。

DonaldShell

希尔排序与前面的排序算法不同，希尔排序把序列看作一个矩阵，分成 m 列，逐列进行排序：

  • m 从某个整数逐渐减为 1
  • 当 m 为 1 时，整个序列将完全有序

因此，希尔排序也被成为递减增量排序（Diminishing Increment Sort）。

矩阵的列数取决于步长序列（step sequence）：

  • 比如，如果步长序列为{1, 5, 19, 41, 109, …} ，就代表依次分成 109 列、41 列、19列、5列、1列进行排序。
  • 不同的步长序列，执行效率也不同

2.2 排序实例

希尔本人给出的步长序列是 n / 2k ，比如 n 为 16 时，步长序列是 {1, 2, 4, 8}。

对下面这个序列进行升序排序：

希尔排序初始序列

分成 8 列进行排序：

分成8列进行排序

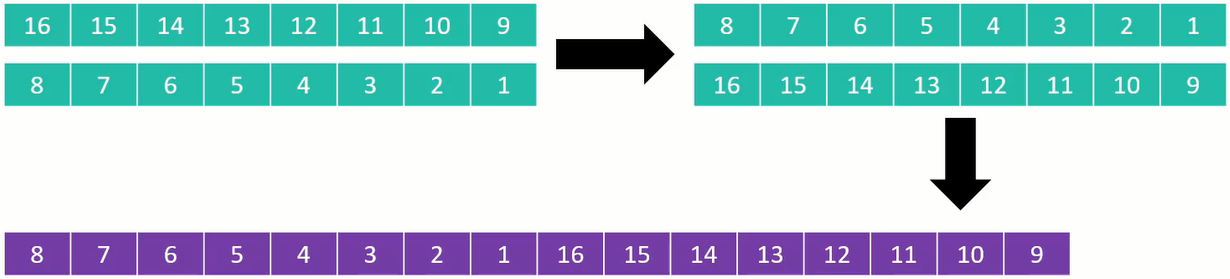
分成 4 列进行排序：

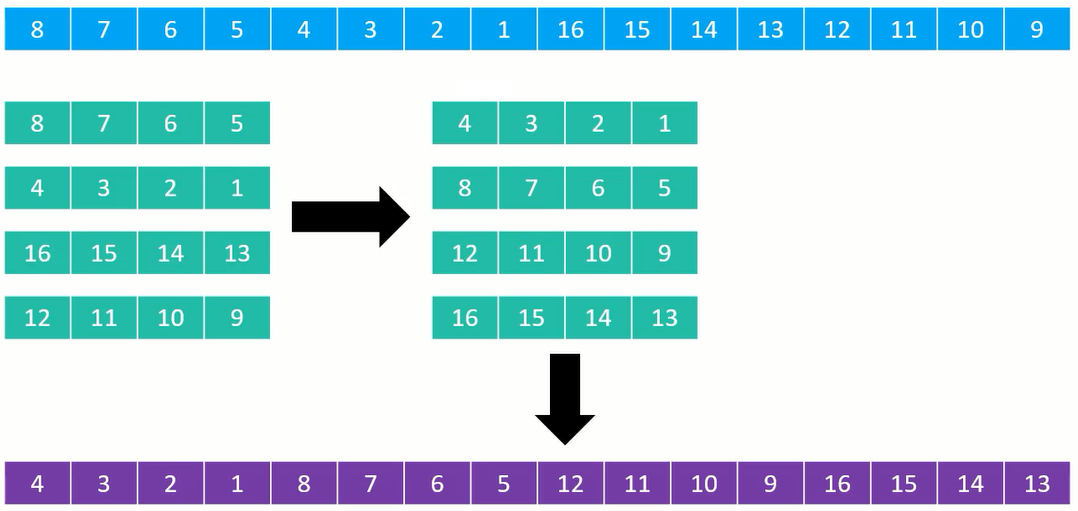
分成4列进行排序

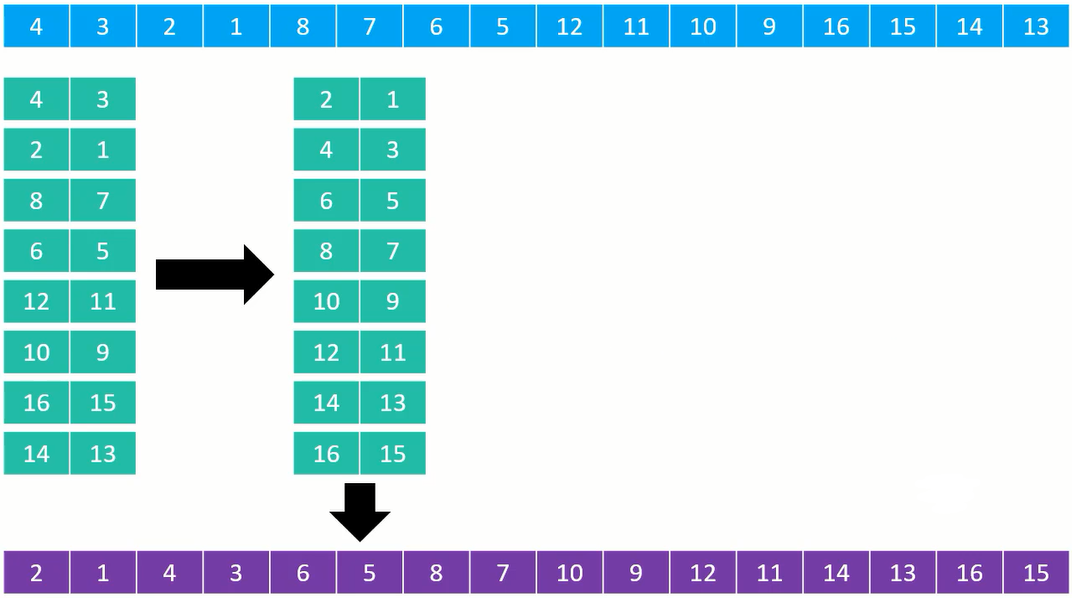
分成 2 列进行排序：

分成2列进行排序

分成 1 列进行排序：

分成1列进行排序

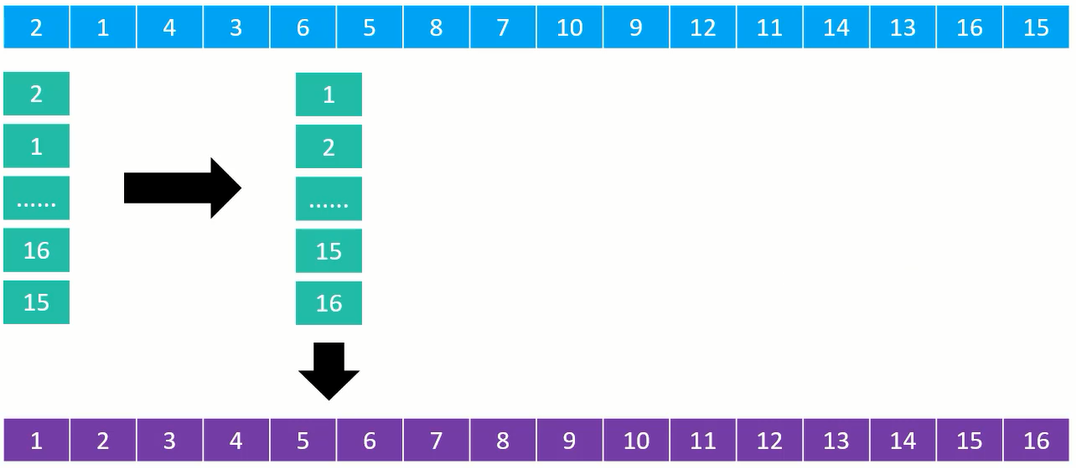
在上面的排序过程中，最后一步是将每个元素独自形成一列进行排序，那么为什么不一开始就分成一列进行排序，前面的分列排序岂不是显得很多余？

其实并不是，从 8 列变为 1 列的过程中，逆序对的数量在不断减少。

因此希尔排序底层一般使用插入排序对每一列进行排序，也有很多资料认为希尔排序是插入排序的改进版。

PS：插入排序的时间复杂度与逆序对的数量成正比关系。

上述给出的实例过于理想，元素数量恰好是 2 的次幂，我们再给出一种一般情况下的实例。

假设有 11 个元素，步长序列是 {1, 2, 5}，分成 5 列进行排序，则有：

分成5列进行排序

假设元素在第 col 列、第 row 行，步长（总列数）是 step

  • 那么这个元素在数组中的索引是 col + row * step
  • 比如 9 在排序前是第 2 列、第 0 行，那么它排序前的索引是 2 + 0 * 5 = 2
  • 比如 4 在排序前是第 2 列、第 1 行，那么它排序前的索引是 2 + 1 * 5 = 7

2.3 编码实现

编写希尔排序时，首先需要创建一个步长序列，我们根据希尔本人给出的步长序列来进行编码。

获得步长序列后，我们需要对原数列进行分列，然后进行排序，比如：

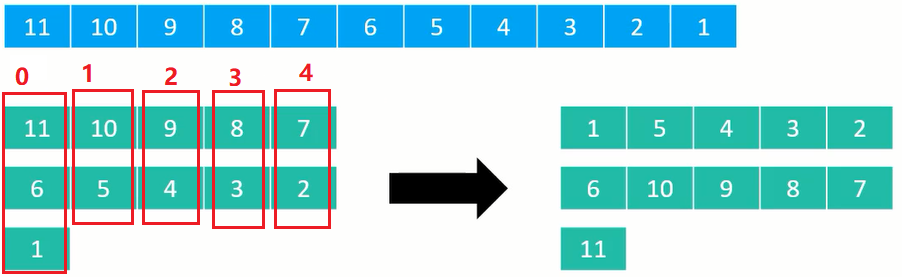
分列后进行排序

分列后对每列进行排序，上图红色粗体数字表示列数，对每列的数据进行排序后可以得到右边的结果。

针对每一列进行的排序，我们可以使用插入排序来实现，至于每列元素索引的获取我们已经在上节末尾给出了。

那么希尔排序编码实现为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
package com.yang.sort;

import java.util.ArrayList;
import java.util.List;

/**
 * @author 默烦
 * @date 2020/8/16
 */
public class ShellSort<E extends Comparable<E>> extends Sort<E> {

    @Override
    protected void sort() {
        List<Integer> stepSequence = shellStepSequence();
        for (Integer step : stepSequence) {
            sort(step);
        }
    }

    /**
     * 分成 step 列进行排序
     *
     * @param step 列数
     */
    private void sort(int step) {
        // col : 第几列, column
        for (int col = 0; col < step; col++) { // 对第col列进行排序
            // col、col+step、col+2*step、col+3*step......
            for (int begin = col + step; begin < array.length; begin += step) {
                int cur = begin;
                while (cur > col && cmp(cur, cur - step) < 0) {
                    swap(cur, cur - step);
                    cur -= step;
                }
            }
        }
    }

    // 获取希尔本人给出的步长序列
    private List<Integer> shellStepSequence() {
        List<Integer> stepSequence = new ArrayList<>();
        int step = array.length;
        while ((step >>= 1) > 0) {
            stepSequence.add(step);
        }
        return stepSequence;
    }
}

复杂度与稳定性

最好情况是步长序列只有 1 ，且序列几乎有序，时间复杂度为 O(n)

最坏的时间复杂度为： O(n4/3) ~ O(n2)，见下文分析

平均时间复杂度取决于步长序列

希尔排序采取原地排序，没有依赖额外存储空间也没有递归调用，因此空间复杂度为： O(1)

希尔排序属于不稳定排序（我们从分列排序示意图可以看出来）。

因为希尔排序是逐列排序的，其稳定性无法控制，也无法通过我们原来的稳定性测试代码测试出来，为了打印结果的准确，我们需要修改稳定性判断isStable()方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private boolean isStable() {
    if (this instanceof SelectionSort) return false;
    if (this instanceof ShellSort) return false;
    Student[] students = new Student[20];
    for (int i = 0; i < students.length; i++) {
        // 创建有序的序列
        students[i] = new Student(i * 10, 10);
    }
    sort(((E[]) students)); // 进行排序
    for (int i = 1; i < students.length; i++) {
        int score = students[i].score;
        int prevScore = students[i - 1].score;
        // 检查序列顺序是否发生改变
        if (score != prevScore + 10) return false;
    }
    return true;
}

然后我们使用上面编写的代码进行测试，生成 3w 个随机数，范围是[1, 30000] ，方法耗时如下：

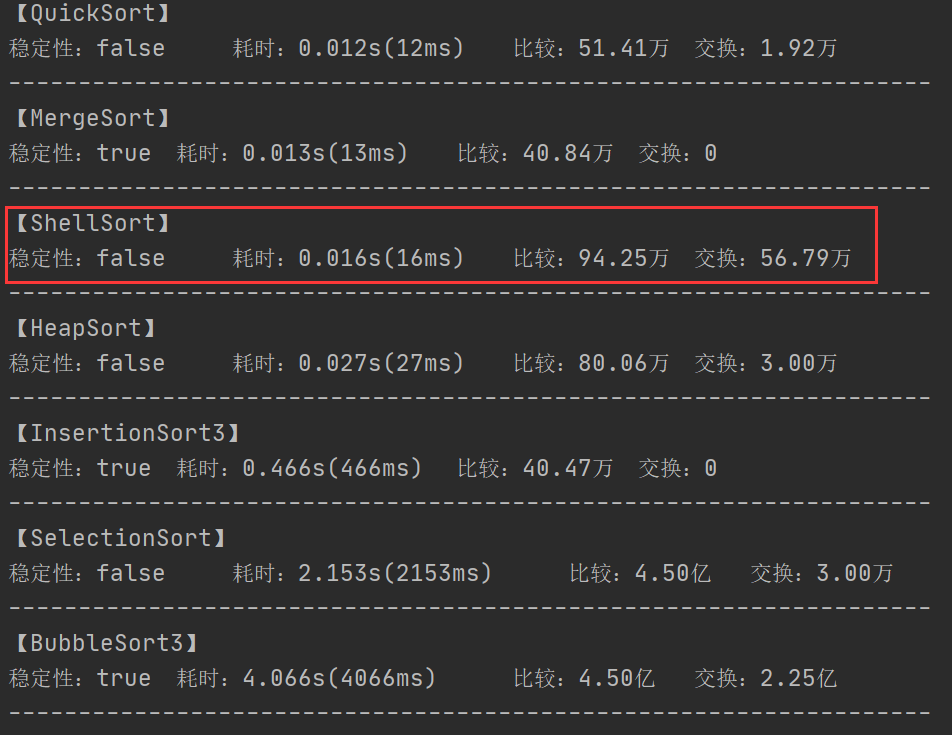
希尔排序测试对比

2.4 步长序列

希尔本人给出的步长序列，最坏情况时间复杂度为O(n2)

1
2
3
4
5
6
7
8
9
// 获取希尔本人给出的步长序列
private List<Integer> shellStepSequence(int count) {
    List<Integer> stepSequence = new ArrayList<>();
    int step = count;
    while ((step >>= 1) > 0) {
        stepSequence.add(step);
    }
    return stepSequence;
}

随着科学家们的研究，目前已知的最好的步长序列，最坏情况时间复杂度为 O(n4/3)，这是由 Robert Sedgewick 在1986年提出的。

已知最好的步长序列公式

代码实现：

最好的步长序列代码实现

将上述代码替换到我们代码中，其它代码不变：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
@Override
protected void sort() {
    // 根据元素数量算出步长序列
    List<Integer> stepSequence = sedgewickStepSequence();
    // 按步长序列划分进行排序
    for (Integer step : stepSequence) {
        sort(step); // 按step进行排序
    }
}

private List<Integer> sedgewickStepSequence() {
    List<Integer> stepSequence = new LinkedList<>();
    int k = 0, step = 0;
    while (true) {
        if (k % 2 == 0) {
            int pow = (int) Math.pow(2, k >> 1);
            step = 1 + 9 * (pow * pow - pow);
        } else {
            int pow1 = (int) Math.pow(2, (k - 1) >> 1);
            int pow2 = (int) Math.pow(2, (k + 1) >> 1);
            step = 1 + 8 * pow1 * pow2 - 6 * pow2;
        }
        if (step >= array.length) break;
        stepSequence.add(0, step);
        k++;
    }
    return stepSequence;
}